生徒が理科大を今年(2024年入試)受験したので、1題紹介します。(1)が解決すると、(2)は1文字消去して1文字で範囲を、(3)は \(x, y\) で表せれば軌跡が求まります。なので、肝心なのは(1)を正しく解答することにあります。(1)ができないと(2)(3)も自動的に落とす厳しい問題。皆さんならどう解きますか?
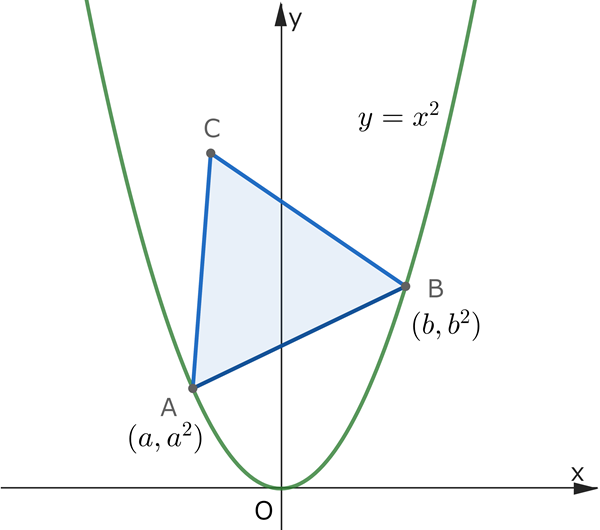
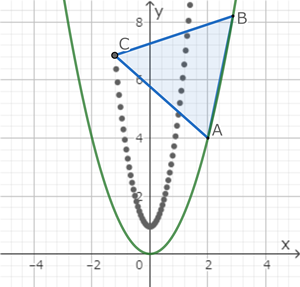
”座標平面において, 曲線 \(y=x^2\) 上に異なる2点 A(\(a, a^2\)), B(\(b, b^2\)) をとり, 線分ABを1辺とする正三角形ABCを考える。ただし, \(a<b\) とし, 点C は A, B, C が反時計回りとなるようにとる。以下の問いに答えよ。
(1) 点C の座標を求めよ。
(2) 点A, B が \(b-a=\dfrac{\sqrt{3}}{3}\) を満たしながら曲線 \(y=x^2\) 上を動くとき, 点C の \(y\) 座標が動く範囲を求めよ。
(3) 点A, B が \(b-a=\dfrac{\sqrt{3}}{2}\) を満たしながら曲線 \(y=x^2\) 上を動くとき, 点C の軌跡を求めよ。”
引用:東京理科大学
複素数を利用して回転後の座標を求めてみます。
【解答例】
C(\(x, y\)) とおくと
\((x-a)+(y-a^2)i=\left\{(b-a)+(b^2-a^2)i \right\}\left(\cos{\dfrac{\pi}{3}}+i\sin{\dfrac{\pi}{3}}\right)\)
\(x+yi=\dfrac{(b+a)-\sqrt{3}(b^2-a^2)}{2}+\dfrac{(b^2+a^2)+\sqrt{3}(b-a)}{2}i\)
よって, 点Cの座標は
\(\left(\dfrac{(b+a)-\sqrt{3}(b^2-a^2)}{2} ,\dfrac{(b^2+a^2)+\sqrt{3}(b-a)}{2} \right)\)・・・(答)
または行列(行列は高校では履修しませんが)を利用すれば
\(\begin{pmatrix}
x-a \\
y-a^2
\end{pmatrix}
=
\begin{pmatrix}
\cos\dfrac{\pi}{3} & -\sin\dfrac{\pi}{3} \\
\sin\dfrac{\pi}{3} & \cos\dfrac{\pi}{3}
\end{pmatrix}
\begin{pmatrix}
b-a \\
b^2-a^2
\end{pmatrix}\)
を解いても良いでしょうか。
(2)
\(b=a+\dfrac{\sqrt{3}}{3}\) より
\(y=\left(a+\dfrac{1}{2\sqrt{3}} \right)^2+\dfrac{7}{12}≧\dfrac{7}{12}\)
よって, \(y≧\dfrac{7}{12}\)・・・(答)
ちなみに, \(x=0\) となっています。
(3)
\(b+a=-4x\)
\(ba=4x^2-\dfrac{3}{16}\) より
\(y=\dfrac{1}{2}\left\{(b+a)^2-2ab \right\}+\dfrac{3}{4}\)
∴ \(y=4x^2+\dfrac{15}{16}\)・・・(答)
※別解で解けた方は是非お問い合せメールフォームより投稿してください。
\(b+a=-4x\)
\(ba=4x^2-\dfrac{3}{16}\) より
\(y=\dfrac{1}{2}\left\{(b+a)^2-2ab \right\}+\dfrac{3}{4}\)
∴ \(y=4x^2+\dfrac{15}{16}\)・・・(答)
※別解で解けた方は是非お問い合せメールフォームより投稿してください。
お問い合わせはこちらから
メール確認後、ご返信いたします
(受付時間 平日9:00~18:00)
(受付時間 平日9:00~18:00)