5 次の(1)から(4)までの各問いに答えなさい。
(1) 1次関数 \(y=2x-1\) について, \(x\) の値が2から5まで増加するときの \(y\) の増加量を求めなさい。
(2)
右の図は, 1次関数 \(y=ax+b\) のグラフです。このとき, \(a, b\) の正負について正しく表しているものを, 次のアからエまでの中から1つ選び, 記号で答えなさい。
ア \(a>0, b>0\) イ \(a>0, b<0\)
ウ \(a<0, b>0\) エ \(a<0, b<0\)
右の図は, 1次関数 \(y=ax+b\) のグラフです。このとき, \(a, b\) の正負について正しく表しているものを, 次のアからエまでの中から1つ選び, 記号で答えなさい。
ア \(a>0, b>0\) イ \(a>0, b<0\)
ウ \(a<0, b>0\) エ \(a<0, b<0\)
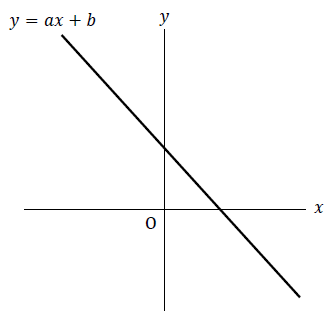
下の表は, ある1次関数についての \(x\) の値とそれに対応する \(y\) の値を表しています。\(y\) を \(x\) の式で表しなさい。
| x | ・・・ | -3 | -1 | 1 | 3 | ・・・ |
| y | ・・・ | -11 | -5 | 1 | 7 | ・・・ |
【解説】
(1) 1次関数の傾き \(a\) は, \(x\) の増加量:\(\Delta x\), \(y\) の増加量:\(\Delta y\) とすると
\(a=\dfrac{\Delta y}{\Delta x}\)
と表せます。
したがって
\(\dfrac{\Delta y}{5-2}=2\)
\(\Delta y=6\)
よって, \(y\) の増加量は6・・・(答)
(2) \(b\) は切片といいます。グラフより, \(a<0, b>0\) とすぐに分かります。 よって, ウ・・・(答)
(3) 表のデータより連立方程式が作れます。
\(\begin{cases} 1=a\cdot 1+b\\ 7=a\cdot 3+b\end{cases}\)
書き直すと
\(\begin{cases} a+b=1\cdots ①\\ 3a+b=7\cdots ②\end{cases}\)
①-②の加減法で解くと
\(a+b=1\)
-) \(\underline{3a+b=7}\)
\(-2a=-6\)
\(a=3\)
これを①に代入すると
\(3+b=1\)
\(b=-2\)
よって, \(y=3x-2\)・・・(答)