茨城県立高校入試 数学３ 解説

３　先生と太郎さんと花子さんの次の会話を読んで, あとの（１）～（３）の問いに答えなさい。

（先生と太郎さんと花子さんの会話）
先生：
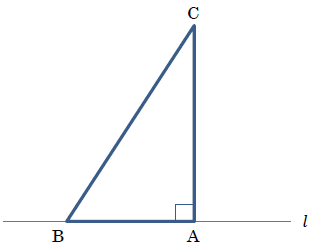
下の図１の△ABCは, ∠ABC=66°, ∠BAC=90°の直角三角形です。
△ABCを直線 \(l\) にそってすべらないように転がしていくことを考えましょう。
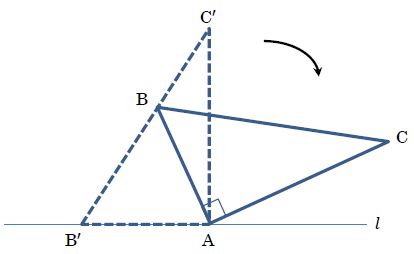
下の図２のように, 点Aを中心に回転させたとき, もとの位置の三角形を△AB’C’とすると, △ABCの頂点Bが, △AB’C’の辺B’C’上にくるときがあります。

太郎：
先生, このときの∠BAB’の大きさは（ア）なので, 図２の△ABCの点Aを中心に時計回りに（ア）だけ回転運動させたことになります。

先生：
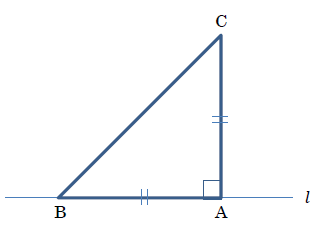
よく気がつきましたね。では次に, 下の図３のように△ABCをAB=ACの直角二等辺三角形にして, 同じように転がしていくことを考えましょう。

太郎：
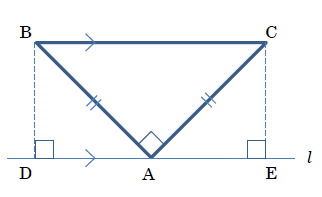
上の図４のように, 直線 \(l\) と辺BCが平行になるときがあります。

花子：
このとき, 点B, Cから直線 \(l\) に垂線をひき, 直線 \(l\) との交点をそれぞれD, Eとすると, △ADB≡△AEC が成りたちそうね。

先生：
では、花子さん, 黒板に証明を書いてください。

花子：
はい。次のように証明できます。
（花子さんの証明）

先生：
そのとおりです。よくできましたね。
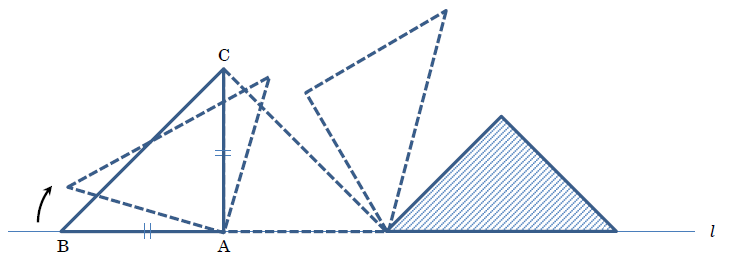
さらに, 図３の直角二等辺三角形ABCを, 下の図５のように, 直線 \(l\) にそってすべらないように, 点Bが再び直線 \(l\) 上にくる斜線の図形の位置まで転がしていくことを考えましょう。

太郎：
点Bが動いた跡にできる線と直線 \(l\) とで囲まれた部分の面積はどうなるのかな。

先生：
では, AB=AC=3cm として, 面積を求めてみましょう。

太郎：
はい。面積を求めると（　ウ　）cm² になりました。

先生：
そのとおりです。よくできましたね。

（１）　会話中の（　ア　）に当てはまる角の大きさを求めなさい。

（２）　会話中の（　イ　）に当てはまる証明を書きなさい。

（３）　会話中の（　ウ　）に当てはまる数を求めなさい。

---

【解説】難度：易しい
(1) △ABB’は二等辺三角形なので, ∠ABB’=∠AB’B=66°
よって、∠BAB’=48°・・・(答)

(2) (証明)
△ADB と △AEC について
仮定より
AB = AC ・・・①
∠ADB = ∠AEC = 90° ・・・②
△ABCは直角二等辺三角形より
∠ABC = ∠ACB・・・③
BC と DE は平行により錯角が等しいので
∠BAD = ∠ABC・・・④
∠CAE = ∠ACB・・・⑤
③④⑤より ∠BAD = ∠CAE・・・⑥

①②⑥より, 斜辺と１鋭角がそれぞれ等しい直角三角形なので
△ADB ≡ △AEC (証明終)

(3)
半径AB=3cm, 中心角４５°のおうぎ形の面積
\(=3\times 3 \times \pi \times \dfrac{1}{4}=\dfrac{9}{4}\pi\)・・・①

△ABCの面積 \(=3\times 3\times \dfrac{1}{2}=\dfrac{9}{2}\)・・・②

半径BC=\(3\sqrt{2}\) cm, 中心角１３５°のおうぎ形の面積
\(=3\sqrt{2} \times 3\sqrt{2} \times \pi \times \dfrac{135}{360}\)
\(=\dfrac{27}{4}\pi\)・・・③

①＋②＋③より求める面積は
\(9\pi +\dfrac{9}{2}\) cm²・・・(答)