半減期

天然に存在する炭素原子は、¹²C, ¹³C, ¹⁴C があります。このように、原子番号が同じで、質量数の異なる原子を互いに同位体（アイソトープ）といいます。このうち、¹⁴C は放射線を放出します。このような原子を放射性同位体（ラジオアイソトープ）といいます。一般に、放射性同位体は原子核が不安定であるため、放射線を出して他の原子に変化します。このことを、崩壊または壊変（物理では崩壊、化学では壊変という表現のようです）といいます。

例えば、¹²C は $\beta$ 壊変で ¹⁴N に変化します。

放射性同位体は医療や農業といった広い分野で利用されています。ここで、放射性同位体を用いた生存年代の測定を紹介します。

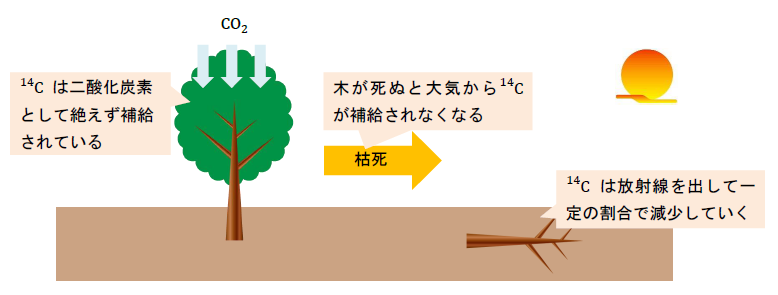
大気中の¹⁴Cは、光合成によって二酸化炭素CO₂として木に取り込まれるため、木に存在する¹⁴Cは大気中と同じ割合に保たれます。

しかし、気が伐採されたり枯れたりすると¹⁴Cが大気から補給されなくなるため、壊変によって木の¹⁴Cは減少していきます。

¹⁴Cの半減期は5730年なので、遺跡から出土した木片に残存している¹⁴Cの割合を測定することで、木が生存していた年代を知ることができます。

これを放射性炭素年代測定といいます。

例えば、遺跡から出土した木片の¹⁴Cの割合を測定したところ、現在の¹⁴Cの割合の $\frac{1}{16}$ であったとします。

この場合、1 ⇒ $\frac{1}{2}$ ⇒ $\frac{1}{4}$ ⇒ $\frac{1}{8}$ ⇒ $\frac{1}{16}$ つまり、5730年×4=22920年となり木片は22920年前のものと考えることができます。

---

例題
遺跡から出土した木片の¹⁴Cの割合を測定したところ、現在の¹⁴Cの割合の $\frac{1}{10}$ であったとします。木片は何年前のものと考えられるか。 ${\log }_{2}10=3.32$ として算出しなさい。

---

【解答】
¹⁴Cの残存量Nは、最初の量をN₀とすると
$N=N_0{\left(\frac{1}{2}\right)}^{\frac{t}{5730}}$
と表せる。
$N=\frac{1}{10}$, $N_0=1$
を代入すると
$\frac{1}{10}={\left(\frac{1}{2}\right)}^{\frac{t}{5730}}$
$2^{\frac{t}{5730}}=10$
$\frac{t}{5730}={\log }_{2}10$
よって、木片は19023.5年前のものと考えられます。・・・(答)