【問題】
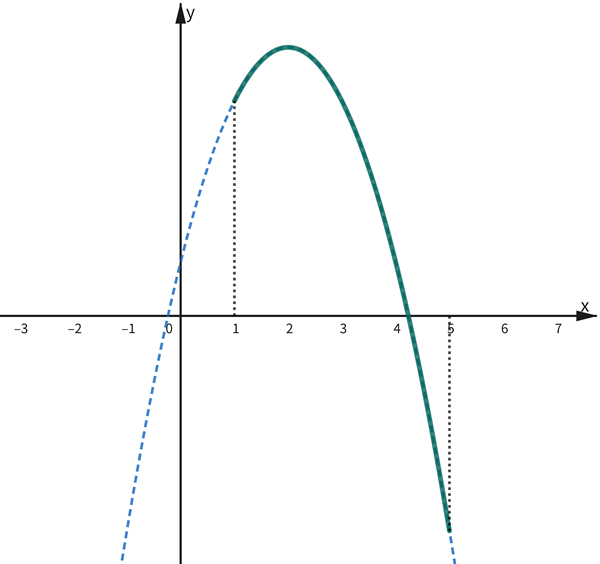
\(y=-x^2+4x+a\) (\(a\)：定数) の \(1≦x≦5\) における \(y\) の最小値が \(1\) のとき、\(a\) の値を求めなさい。
【解答】
平方完成すると
\(y=-(x^2-4x)+a\)
\(y=-(x-2)^2+4+a\)
頂点の座標は \((2,4+a)\)
グラフより
\(x=5\) のとき最小値となるので
\(-5^2+4\cdot 5+a=1\)
\(a=6\)・・・（答）