【問題】
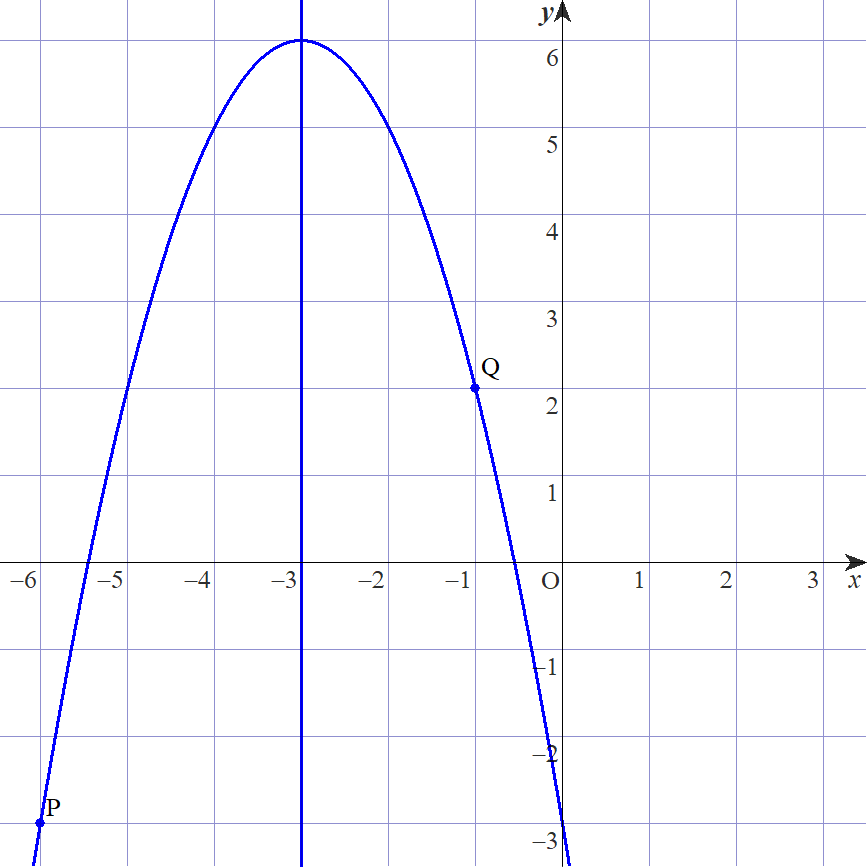
軸が \(x=-3\) で、2点 \((-6, -3), (-1, 2)\) を通る2次関数を求めなさい。
【解答】
軸が \(x=-3\) なので \(y=a(x+3)^2+b\) と表せます。
\((x, y)=(-6, -3), (-1. 2)\) を代入すると
\(-3=9a+b\)・・・①
\(2=4a+b\)・・・②
①, ②の連立方程式を解くと
\(a=-1, b=6\)
よって、\(y=-(x+3)^2+6\)・・・(答)
軸が \(x=-3\) なので \(y=a(x+3)^2+b\) と表せます。
\((x, y)=(-6, -3), (-1. 2)\) を代入すると
\(-3=9a+b\)・・・①
\(2=4a+b\)・・・②
①, ②の連立方程式を解くと
\(a=-1, b=6\)
よって、\(y=-(x+3)^2+6\)・・・(答)