ボルツマン定数とは
ボルツマン定数は気体の分子運動論で重要な定数の一つです。
また、現在の熱力学温度の単位K(ケルビン)の定義は、ボルツマン定数 \(k\) を単位J・K-1で表したときに、その数値を \(1.380 649\times 10^{-23}\) と定めることによって定義されています。

\(k=\dfrac{R}{N_A}=\dfrac{8.31}{6.02\times 10^{23}}\fallingdotseq 1.38\times 10^{-23}\) J/K
ここで、気体分子の平均運動エネルギーを算出していきます。下記の導出の流れは大事です。
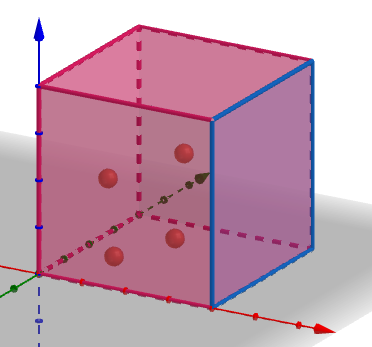
図のような1辺の長さ \(L\) [m]、体積 \(V=L^3\) [m3] の立方体の容器に、質量 \(m\) [kg] の分子 \(N\) 個からなる理想気体を入れます。このとき、分子は他の分子とは衝突せず等速直線運動し、壁との衝突は弾性衝突するものとします。
1回の衝突で壁Sが分子から受ける力積
壁Sに衝突する直前の分子の速度を \(x\) 軸方向のみに着目し \(v_x\) とすると、衝突後、分子の速度は \(-v_x\) となるので、分子が壁から受ける力積は
\(F\Delta t =-v_X-v_x=-2v_x\)
壁が分子から受ける力積は、作用・反作用の法則より \(2mv_x\) [N・s]・・・① となります。
分子が壁Sと衝突するまでの時間
分子は \(2L\) [m] ごとに壁Sと衝突するので、衝突の周期は
\(\dfrac{2L}{v_x}\) [s]・・・②
となります。
壁Sが1つの分子から受ける平均の力
時間 \(t\) の間に分子が壁Sに衝突する回数は
\(t\div \dfrac{2L}{v_x}=\dfrac{v_x t}{2L}\) [回](∵②)・・・③
であるから、時間 \(t\) の間に壁Sが1つの分子から受ける力積は
\(2mv_x \times \dfrac{v_x t}{2L}=\dfrac{m{v_x}^2}{L}t\)・・・④(∵①, ③)
となります。
したがって、時間 \(t\) の間に壁Sが1つの分子から受ける平均の力の大きさ \(f\) は
\(f=\dfrac{m{v_x}^2}{L}\)・・・⑤(∵④)
となります。
壁Sが \(N\) 個の分子から受ける圧力
壁Sが \(N\) 個の分子から受ける平均の力の大きさは、\(v_x\) の平均を \(\overline{v_x}\) とすると⑤より
\(F=N\times \dfrac{m\overline{{v_x}^2}}{L}=\dfrac{Nm\overline{{v_x}^2}}{L}\)・・・⑥(∵⑤)
したがって、気体の圧力 \(p\) は
\(p=\dfrac{F}{L^2}=\dfrac{Nm\overline{{v_x}^2}}{L^3}=\dfrac{Nm\overline{{v_x}^2}}{V}\)・・・⑦
ここで、
\(\overline{v^2}=\overline{{v_x}^2}+\overline{{v_y}^2}+\overline{{v_z}^2}\)
であり、分子の運動はどの方向にも均等で偏りがないと考えると、
\(\overline{{v_x}^2}=\overline{{v_y}^2}=\overline{{v_z}^2}\)
よって、\(\overline{{v_x}^2}=\dfrac{\overline{{v}^2}}{3}\)・・・⑧
⑦, ⑧より
\(p=\dfrac{Nm\overline{{v}^2}}{3V}\)
\(pV=\dfrac{Nm\overline{{v}^2}}{3}\)
ここで、気体の状態方程式 \(pV=nRT\) より
\(\dfrac{Nm\overline{{v}^2}}{3}=nRT\)
ゆえに、理想気体の分子1個あたりの運動エネルギーは
\(\dfrac{1}{2}m\overline{{v}^2}=\dfrac{3}{2}\dfrac{nRT}{N}\)
\(N=nN_A\) であるから、
\(\dfrac{1}{2}m\overline{{v}^2}=\dfrac{3}{2}\dfrac{nRT}{nN_A}=\dfrac{3}{2}\dfrac{R}{N_A}T\)
ここで、\(k=\dfrac{R}{N_A}\)(ボルツマン定数) と置くと
\(\dfrac{1}{2}m\overline{{v}^2}=\dfrac{3}{2}kT\)・・・⑨
⑨式より、理想気体の分子の平均の運動エネルギーは、分子の種類によらず絶対温度 \(T\) によって決まることが導出できました。