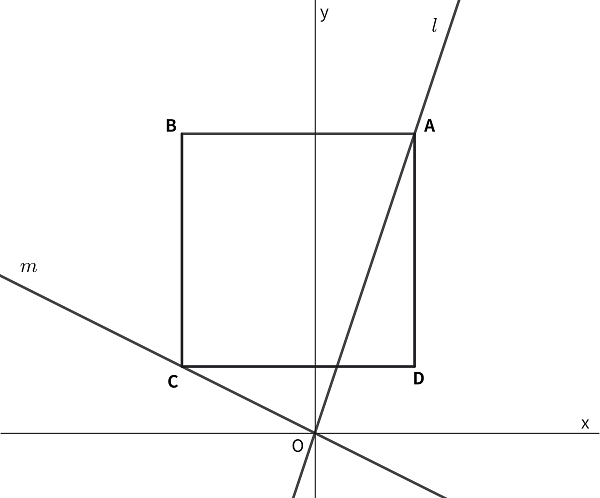
【問題】
図で、直線 \(l, m\) は
\(l: y=3x\)
\(m: y=-\dfrac{1}{2}x\)
です。
四角形ABCDは正方形で辺ABは \(x\)軸に平行、AB = 6 cm であるとき、点 A の \(x\) 座標を求めなさい。
【解答】
A\((a, 3a)\) と置くと
C\((a-6, 3a-6)\)
点Cは、\(m\) 上の点なので
\(3a-6=-\dfrac{1}{2}(a-6)\)
∴ \(a=\dfrac{18}{7}\)・・・(答)