【問題】
\(y\) は \(x\) の２乗に比例し、\(x\) の値が２から４まで増加するときの変化の割合がー１８となります。
\(x\) の変域が、\(-1≦x≦2\) のときの \(y\) の変域を求めなさい。
【解答】
\(y\) は \(x\) の２乗に比例するので
\(y=ax^2\) とおくと
\(x:2 → 4\)
\(y:4a → 16a\)
したがって、変化の割合は
\(\dfrac{\Delta y}{\Delta x}=\dfrac{12a}{2}=6a\)
\(6a=-18\)
\(a=-3\)
よって、式は
\(y=-3x^2\) となります。
\(x\) の変域が、\(-1≦x≦2\) のときのグラフを描くと
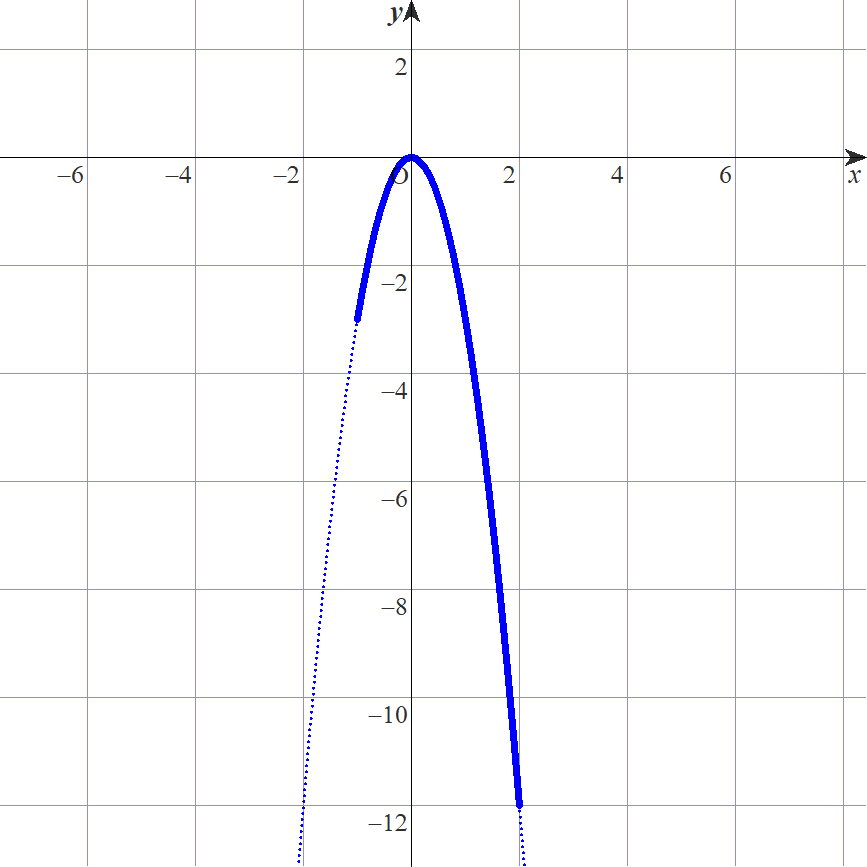
ゆえに、\(y\) の変域は
\(-12≦y≦0\)・・・(答)