媒介変数をうまく利用することで、計算量を大幅に減らすことができます。
【問題】
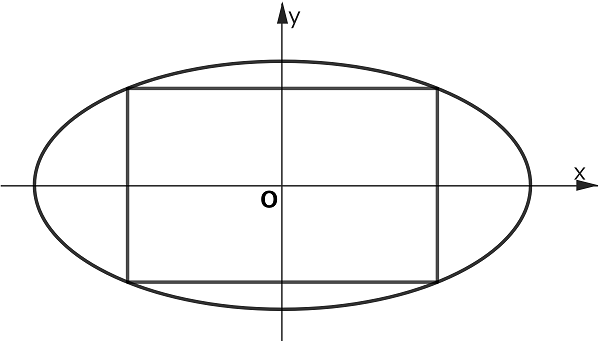
図のように、楕円 \(\dfrac{x^2}{4}+y^2=1\) に内接し、\(x\) 軸、\(y\) 軸に平行な辺をもつ面積の最大値を求めなさい。
【解答1】
求める面積を \(S\) とします。対称性より第1象限部分の面積 \(\dfrac{S}{4}\) の最大値を求めていきます。
長方形の横の長さを \(x\) \((0<x<2)\) とすると
長方形の縦の長さは \(y=\sqrt{1-\dfrac{x^2}{4}}\) となるので、
\(\dfrac{S}{4}=x \sqrt{1-\dfrac{x^2}{4}}=\sqrt{x^2-\dfrac{x^4}{4}}\)
ここで、\(f(x)=x^2-\dfrac{x^4}{4}\) と置き、\(f(x)\) の最大値を考えます。
\(x^2=X\) \((0<X<4)\) と置くと
\(f(x)=X-\dfrac{X^2}{4}\)
\(=-\dfrac{1}{4} \left( X-2 \right)^2 +1\)
よって、\(X=2\) のとき、\(f(x)\) は最大値 \(1\) となります。
したがって、
\(\dfrac{S}{4}=\sqrt{1}=1\)
∴ \(S\) の最大値は \(4\)・・・(答)
【解答2】
\(x=2\cos \theta\)、\(y=\sin \theta\) とおくと
\(\dfrac{S}{4}=2\cos\theta \sin \theta=\sin 2\theta\)
\(S=4\sin2\theta \leq 4\)
∴ \(S\) の最大値は \(4\)・・・(答)